Question:

Preface：

本文解法只是众多解法中的一种，但其出现在官方的标准解答中，反倒可以窥见其设计意图。

而本文解法以其罕见的思路入围我的导数TOP10。

当时老师介绍说是隔壁2班的同学考场复现了，现在回想起依然很佩服。

Answer for (2) :

因为
\[ f(x) = x^{2}\,\bigl(\frac{\ln x + 1}{x}\bigr) - a \quad (x>0), \] 设
\[ g(x) = \frac{\ln x + 1}{x} - a \quad(x>0), \] 所以 \(f(x)\) 的零点即为 \(g(x)\) 的零点。

因为
\[ g'(x) = -\,\frac{\ln x}{x^{2}}. \]

  • 当 \(x \in (0,1)\) 时，\(g'(x) > 0\)，\(g(x)\) 单调递增；
  • 当 \(x \in (1,\infty)\) 时，\(g'(x) < 0\)，\(g(x)\) 单调递减。

因为 \(g(x)\) 有两个零点，则必有 \(g(1)=1-a>0\)，且 \(x \to \infty\) 时 \(g(x)\to -a<0\)，
得 \(0 < a < 1.\)

因为
\[ g\!\bigl(\tfrac{1}{e}\bigr) = -\,a < 0, \]
所以
\[ \tfrac{1}{e} < x_{1} < 1 < x_{2}. \]

依函数关系
\[ g(x_{1}) - g\bigl(2 - x_{1}\bigr), \] 定义
\[ F(x) = g(x) - g\bigl(2 - x\bigr), \quad \Bigl(\tfrac{1}{e}<x<1\Bigr). \] 则其导数为
\[ F'(x) = -\frac{\ln x}{x^{2}} - \Bigl[ \frac{\ln(2 - x)}{(2 - x)^{2}} \Bigr] = \frac{-\ln x}{x^{2}} + \frac{-\ln(2 - x)}{(2 - x)^{2}}. \]

因为 \((2 - x)^{2} > x^{2}\) 且 \(\ln(2 - x) < \ln x\)， 所以\(F'(x)>\frac{-\ln x}{x^{2}}+ \frac{-\ln(2 - x)}{x^{2}}.\) 所以 \(F'(x) > 0.\) 所以 \(F(x)\) 在 \(\bigl(\tfrac{1}{e},\,1\bigr)\) 上单调递增。
所以 \(F(x) < F(1) = 0.\)

于是
\[ g(x) - g(2 - x) < 0, \] 进而
\[ g(x_{1}) < g\bigl(2 - x_{1}\bigr), \quad g(x_{2}) < g\bigl(2 - x_{2}\bigr). \]

因为 \(\tfrac{1}{e}\)<\(x_{1}<1<x_{2}\)，则 \(2 - x_{1}\) > \(1\)。

又因为 \(g(x)\) 在 \((1,\infty)\) 上单调递减，

所以 \(x_{2}\) > \(2 - x_{1}\)，即 \(x_{1}\) + \(x_{2}\) > \(2.\)

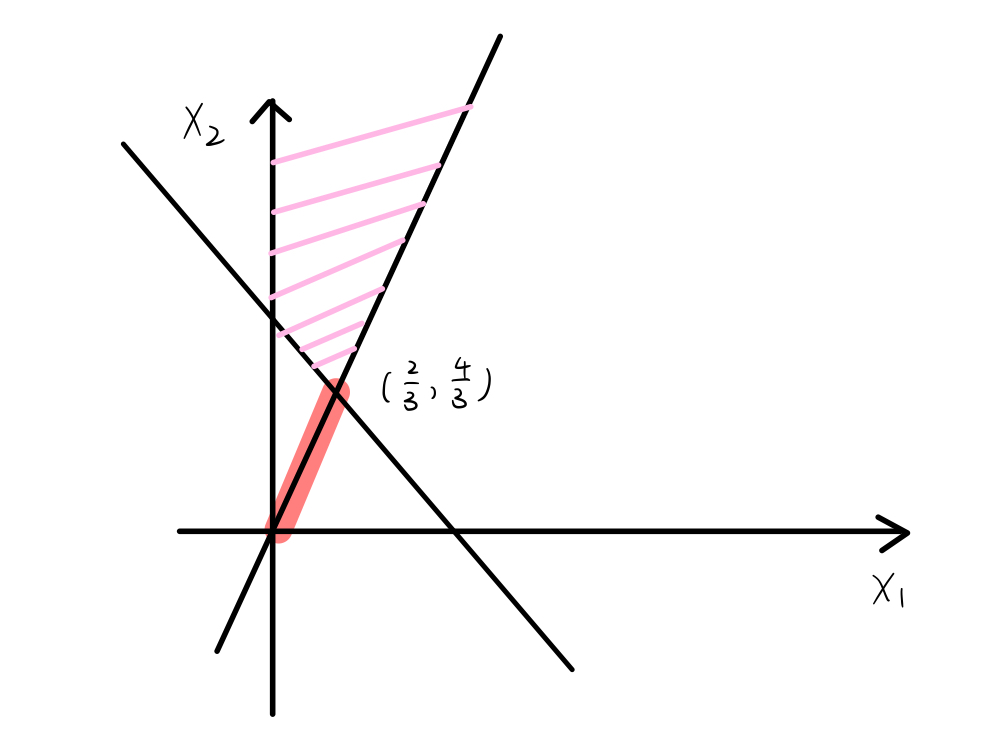
结合条件 \(x_{2} > 2\,x_{1}\) 可知，满足条件的点 \(\bigl(x_{1},x_{2}\bigr)\) 必在不等式组

\[ \begin{cases} x_{1} + x_{2} > 2,\\ x_{2} > 2\,x_{1}, \end{cases} \]

表示的平面区域内，且 \(\tfrac{1}{e}\)<\(x_{1}<1.\)

由 \(x_{1} + x_{2} = 2\) 和 \(x_{2} = 2\,x_{1}\) 相交点

\[ P\Bigl(\tfrac{2}{3},\,\tfrac{4}{3}\Bigr). \]

满足条件的点 \(\bigl(x_{1},\,x_{2}\bigr)\) 到原点的距离
\[ \sqrt{x_{1}^{2} + x_{2}^{2}} = \sqrt{\tfrac{4}{9} + \tfrac{16}{9}} = \sqrt{\tfrac{20}{9}} = \tfrac{2\,\sqrt{5}}{3}. \]

因为
\[ \Bigl(\tfrac{2\,\sqrt{5}}{3}\Bigr)^{2} - \Bigl(\tfrac{4}{e}\Bigr)^{2} = \frac{20\,e^{2} - 144}{\,9\,e^{2}\,} > 0, \]

得
\[ \tfrac{2\,\sqrt{5}}{3} > \tfrac{4}{e}, \]

所以
\[ \sqrt{x_{1}^{2} + x_{2}^{2}} > \tfrac{4}{e}. \]

如图