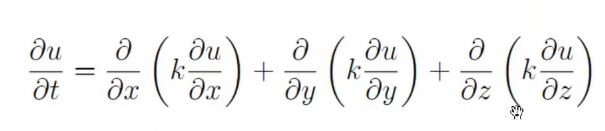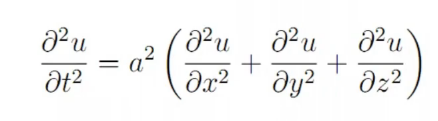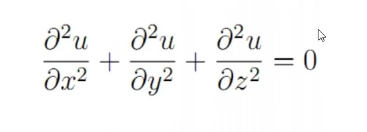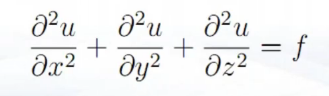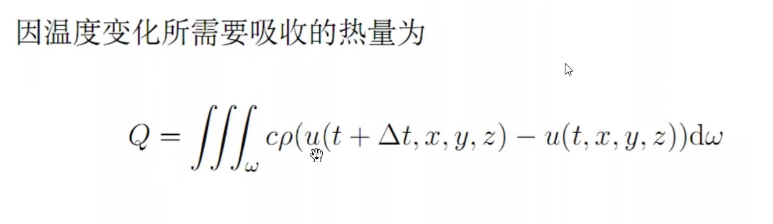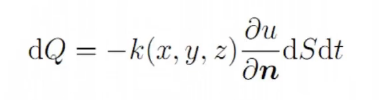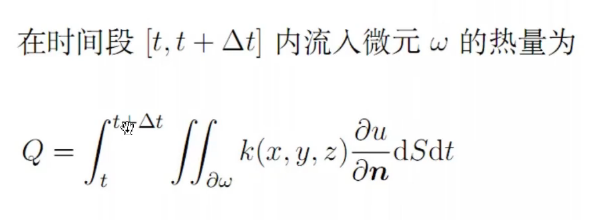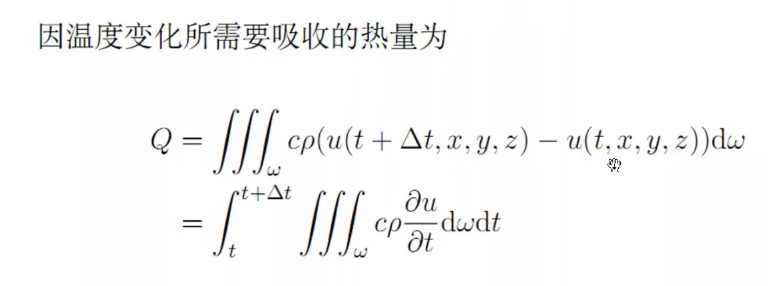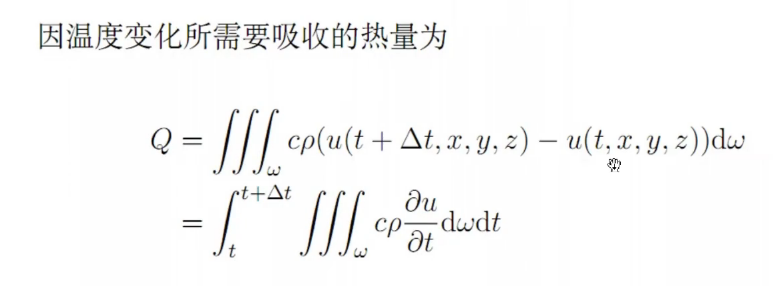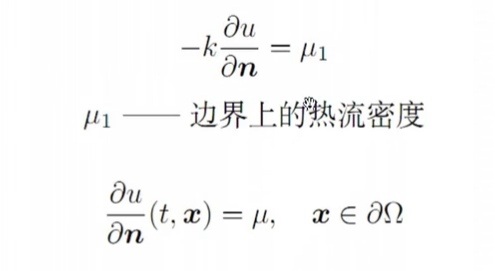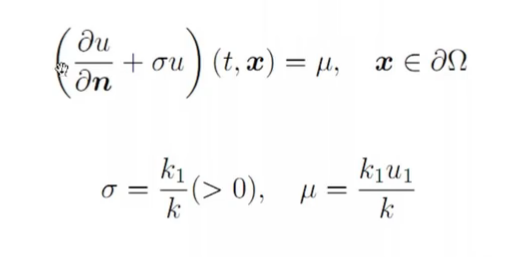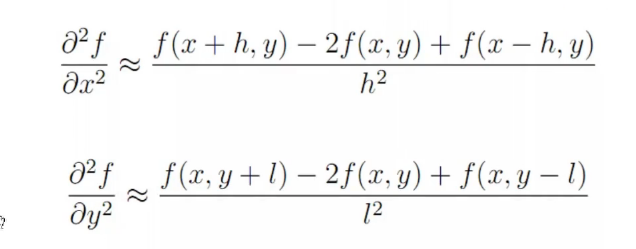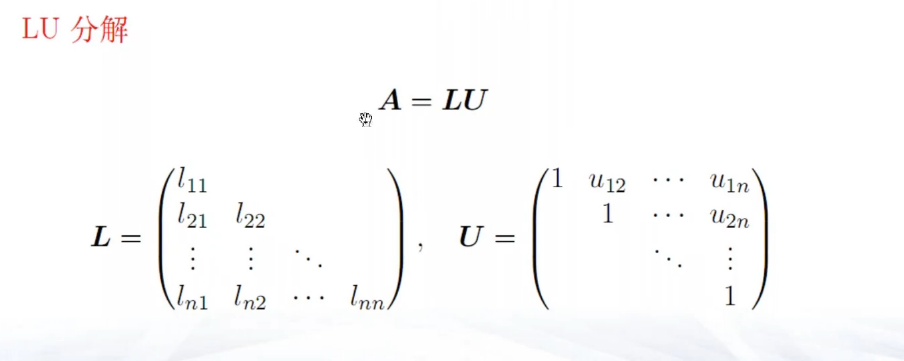引言

实际问题 - 确定性问题：1）连续问题 2）离散问题 - 随机性问题

对于连续问题，可以用常微分方程模型也可以用偏微分方程模型

偏微分方程模型

常见的模型

  • 1）热传导方程

研究热量，温度的变化情况

也可以描述分子扩散的情况

  • 2）波动方程

橡皮筋的波动

  • 3）调和方程

温度不随时间变化而变化

Poisson 方程

引入热源

偏微分方程的类型

  • 热传导方程——抛物线方程
  • 波动方程——双曲线方程
  • 调和方程——椭圆形方程

模型的建立——微元法

时间微元：[t,t + delta t]

空间微元：w=[x,x+ delta x] × [y,y+ delta y] × [z,z+ delta z]

Fourier热传导定律

在时间微元dt内沿面积微元dS的法线方向n流过此面积微元的热量为：

梯度即表示与两边温度差成正比

k为热传导系数

统一空间和时间积分：

面积分变体积分

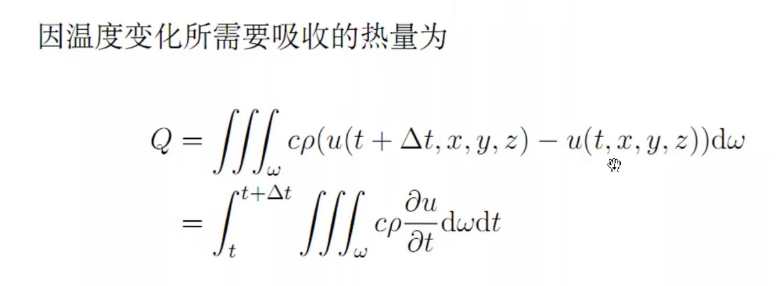
热量守恒定律

定解条件

初始条件：t=0；u=phi(x,y,z)

边界条件
  • Dirichlet 边界条件(第一类边界条件)

u(t,x)=myu，myu为边界上的温度

  • Neumann边界条件(第二类)

  • Robin边界条件(第三类)

理论上来说，给了一种边界条件，那么存在解是唯一的，其他两条边界条件不能随便给。

数值计算

偏微分方程的数值计算方法：

  • 有限差分法
  • 有限元素法

有限差分法就是用差商代替导数，从而将微分方程转换为代数方程组的一种数值计算方法。

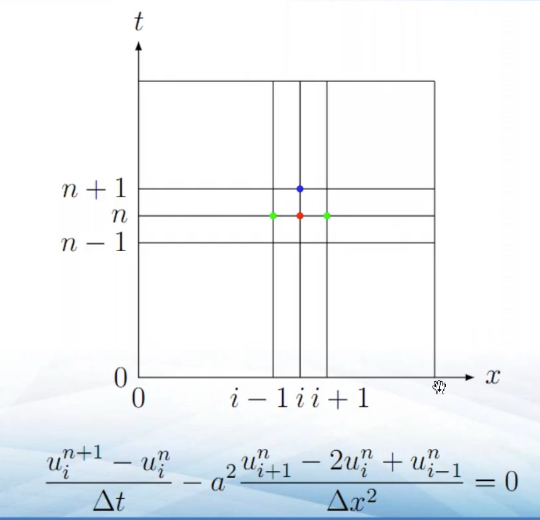
偏微分二阶差商：

举例：

表示该点的温度

为了知道n+1，我们需要知道n；为了知道n，我们需要知道n—1,从而推到初值。

显式差分格式

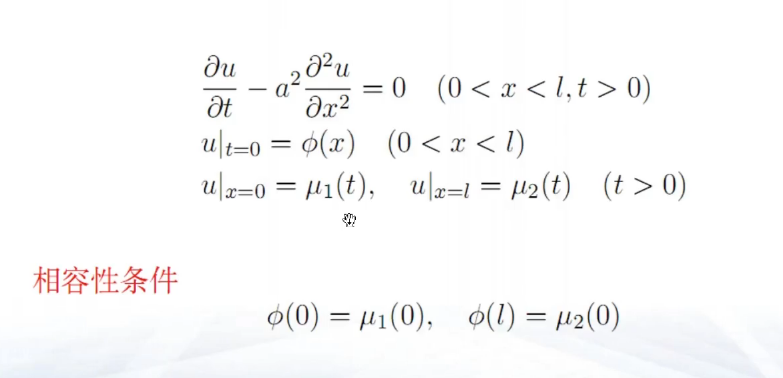
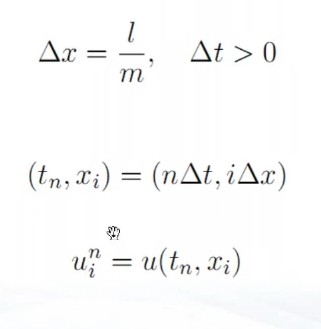
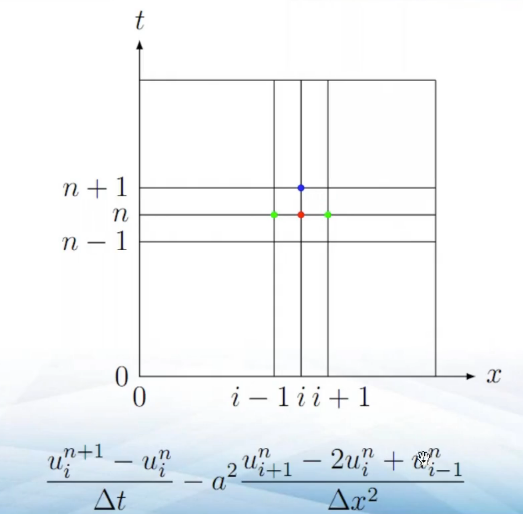
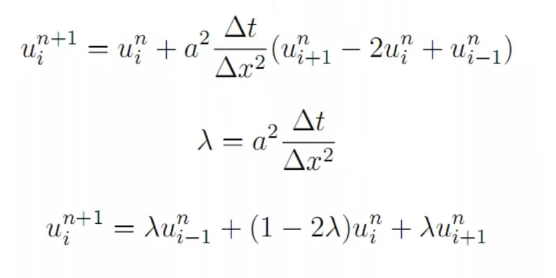
利用边界条件 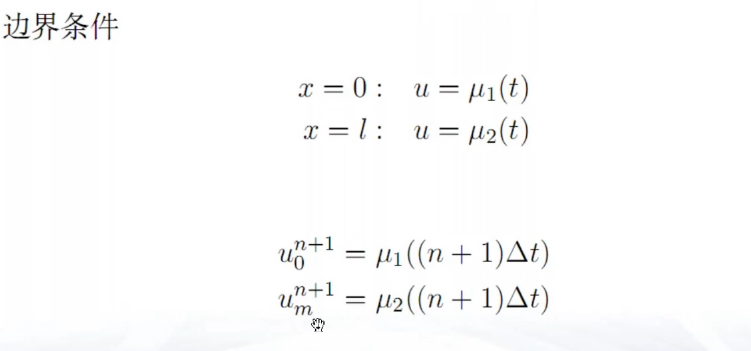再利用显式差分格式

条件稳定：

如果不想受条件稳定限制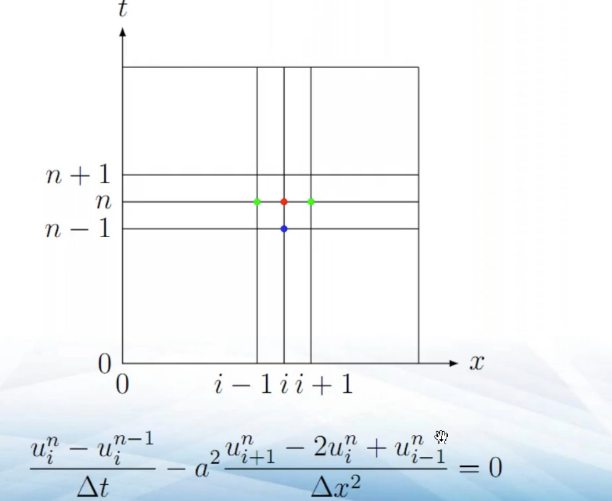： 这时，我们不知道n时刻的温度，所以有3个未知量，不能用显式差分

我们for(i=1;i＜n;i++)得到n-1个方程，n+1个变量

所以，我们选择增加方程来求解，即边界条件的方程。

线性方程组求解

高斯消去

LU分解

计算量： - 分解过程O(n^3) - 回代过程O(n^2)

追赶法

三对角线性方程组

O(n)

赛题

2018A