PyTorch深度学习实践
1、overview
How to develop learning system?
- 基于规则的系统： 输入 -> 手工设计程序 -> 输出
- 传统机器学习 输入 -> 手工设计特征 -> 映射 -> 输出
- 表示学习 特征不再手工提取
深度学习: 输入->简单特征->特征提取器->映射输出 (End2End:模 型可以直接利用输入数据而不需要其他处理)
神经网络简史
Why PyTorch
- Dynamical
1）More flexible 2）Easy to debug 3）Intuitive and cleaner code
- More neural networkic
Write code as network works/ AutoGrad for forward or backward.
2、线性模型
DataSet(数据集) -> Model(模型) -> Training(训练) -> inferring(推理)
1 例子引入
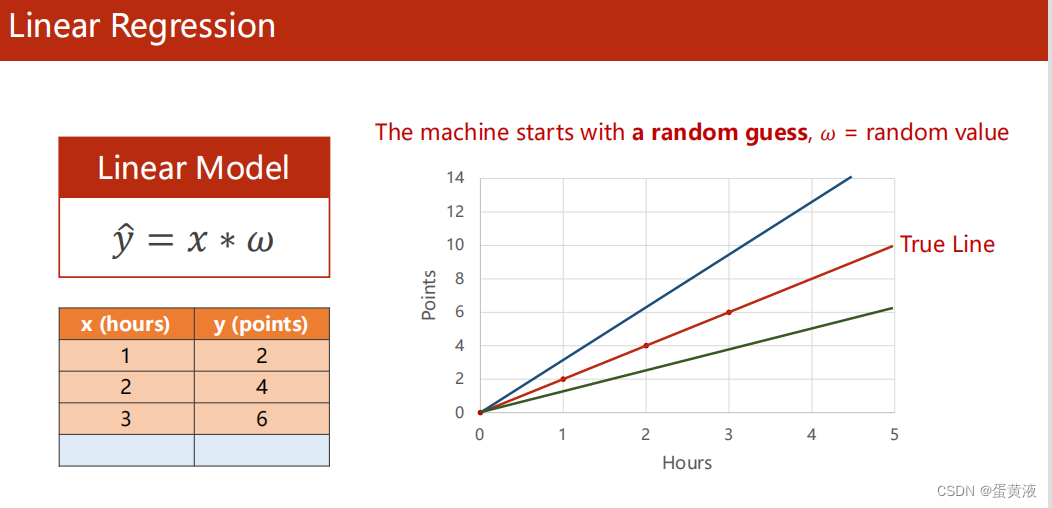
已知数据集学习时间x[1，2，3] 成绩y[2，4，6]，测试数据集x=4,y=?
1 | 此时数据集分为训练数据集和测试数据集 |
2 线性模型
获取最优的线性模型：因为此时数据集较少采用简单的线性模型。随机选取w以后，计算损失值，然后不停调整w的值（在某个范围内穷举）使得损失值最小
Training Loss针对一个样本
Mean Square Error（MSE平均平方误差）针对整个训练集
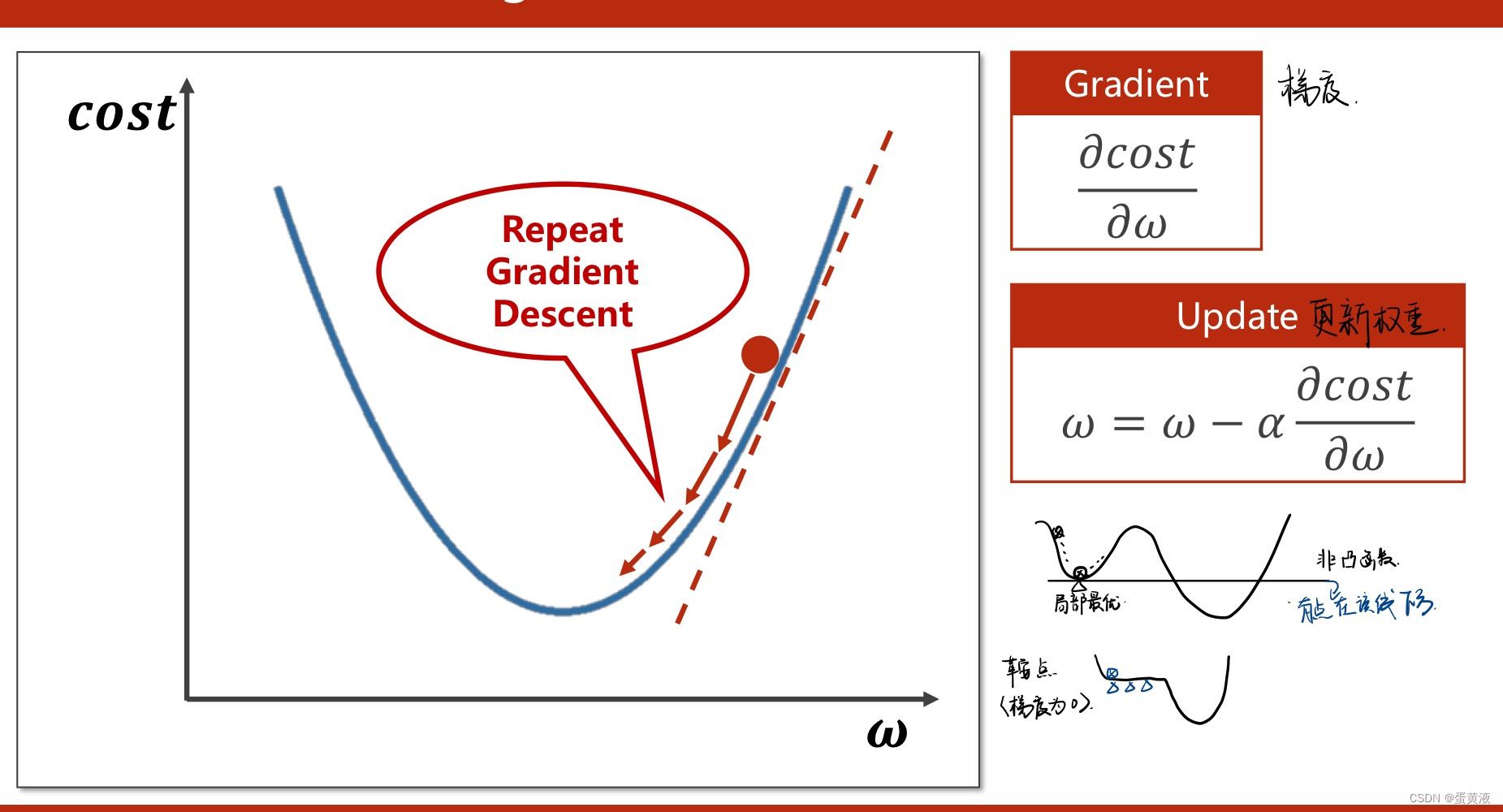
3 Gradient_Descent(梯度下降法)
利用了贪心的思想，查找当前下降最快的位置
梯度下降法的基本思想可以类比为一个下山的过程。 假设这样一个场景：一个人被困在山上，要想快速下山就要寻找最陡峭的地方。首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处；同理上山也是如此，只是这时候就变成梯度上升算法了
梯度下降的基本过程就和下山的场景很类似。
首先，我们有一个可微分的函数。这个函数就代表着一座山。我们的目标就是找到这个函数的最小值，也就是山底。根据之前的场景假设，最快的下山的方式就是找到当前位置最陡峭的方向，然后沿着此方向向下走，对应到函数中，就是找到给定点的梯度 ，然后朝着梯度相反的方向，就能让函数值下降的最快！因为梯度的方向就是函数之变化最快的方向(在后面会详细解释)
所以，我们重复利用这个方法，反复求取梯度，最后就能到达局部的最小值，这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向，也就是场景中测量方向的手段。那么为什么梯度的方向就是最陡峭的方向呢？
在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率
在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向
到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，所以我们只要沿着梯度的方向一直走，就能走到局部的最低点
梯度下降
在线性模型中采用了穷举法，但是对于数据集较大的时候穷举不可行，因此提出梯度下降进行优化。
随机选取一个点，计算梯度，并朝着函数值下降最快的方向走，并且更新w值。
代码：
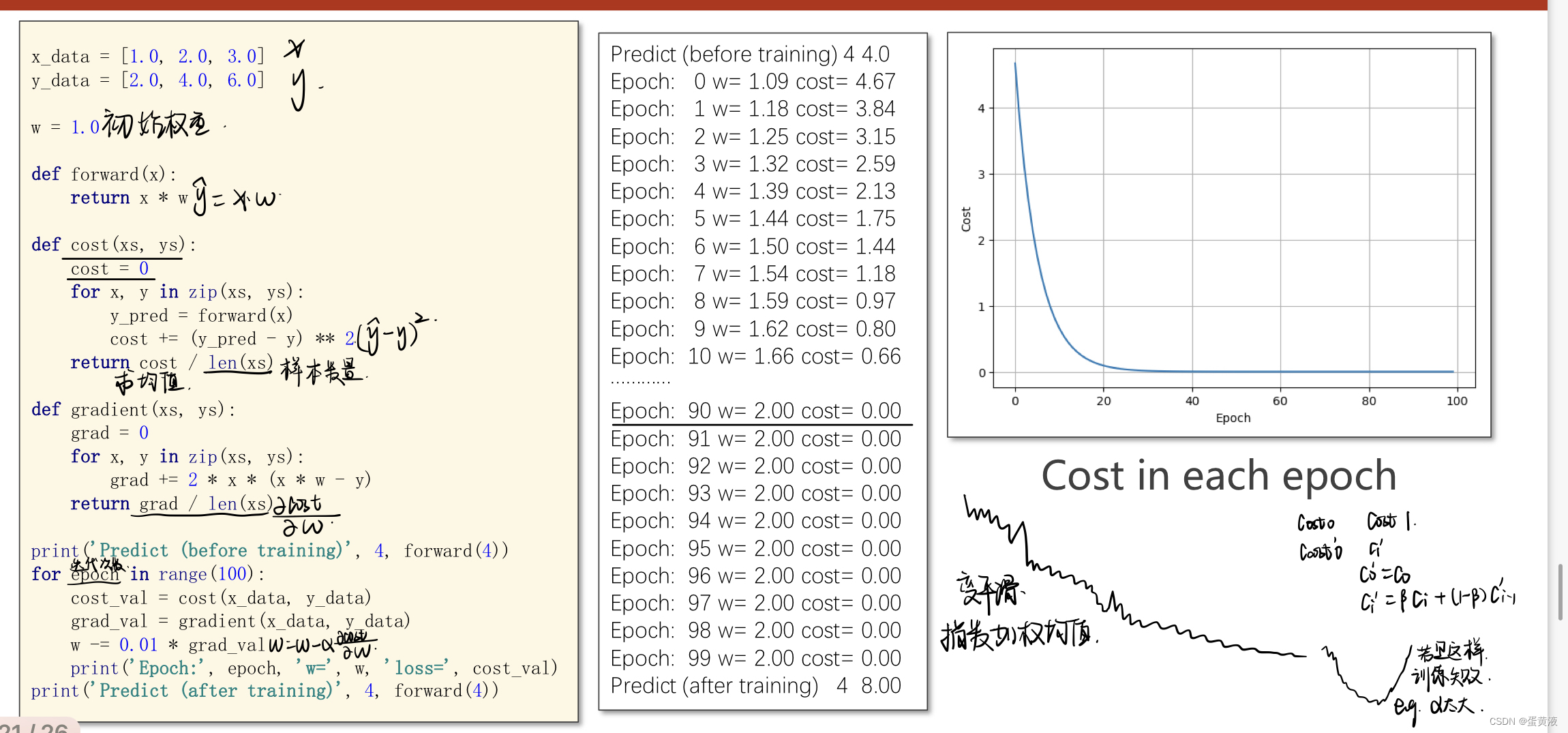
随机梯度下降SDG
梯度下降法遇到鞍点无法跳出，但是随机梯度下降可能会跳跃鞍点
SGD算法是从样本中随机抽出一组，训练后按梯度更新一次，然后再抽取一组，再更新一次，在样本量及其大的情况下，可能不用训练完所有的样本就可以获得一个损失值在可接受范围之内的模型了。
这里的随机是指每次迭代过程中，样本都要被随机打乱，打乱是有效减小样本之间造成的参数更新抵消问题。
对梯度下降和随机梯度下降综合一下获取更好的性能
对数据进行分组mini-batch：组内梯度下降，组间随机梯度下降
Mini batch
为了提高效率，我们可以把样本分成等量的子集。 例如我们把100万样本分成1000份， 每份1000个样本， 这些子集就称为mini batch。mini-batch的大小一般取2的n次方
然后我们分别用一个for循环遍历这1000个子集。 针对每一个子集做一次梯度下降。 然后更新参数w和b的值。接着到下一个子集中继续进行梯度下降。 这样在遍历完所有的mini batch之后我们相当于在梯度下降中做了1000次迭代。 我们将遍历一次所有样本的行为叫做一个 epoch，也就是一个世代。 在mini batch下的梯度下降中做的事情其实跟full batch一样，只不过我们训练的数据不再是所有的样本，而是一个个的子集。 这样在mini batch我们在一个epoch中就能进行1000次的梯度下降，而在full batch中只有一次。 这样就大大的提高了我们算法的运行速度。
梯度下降
简单线性模型的完整计算图
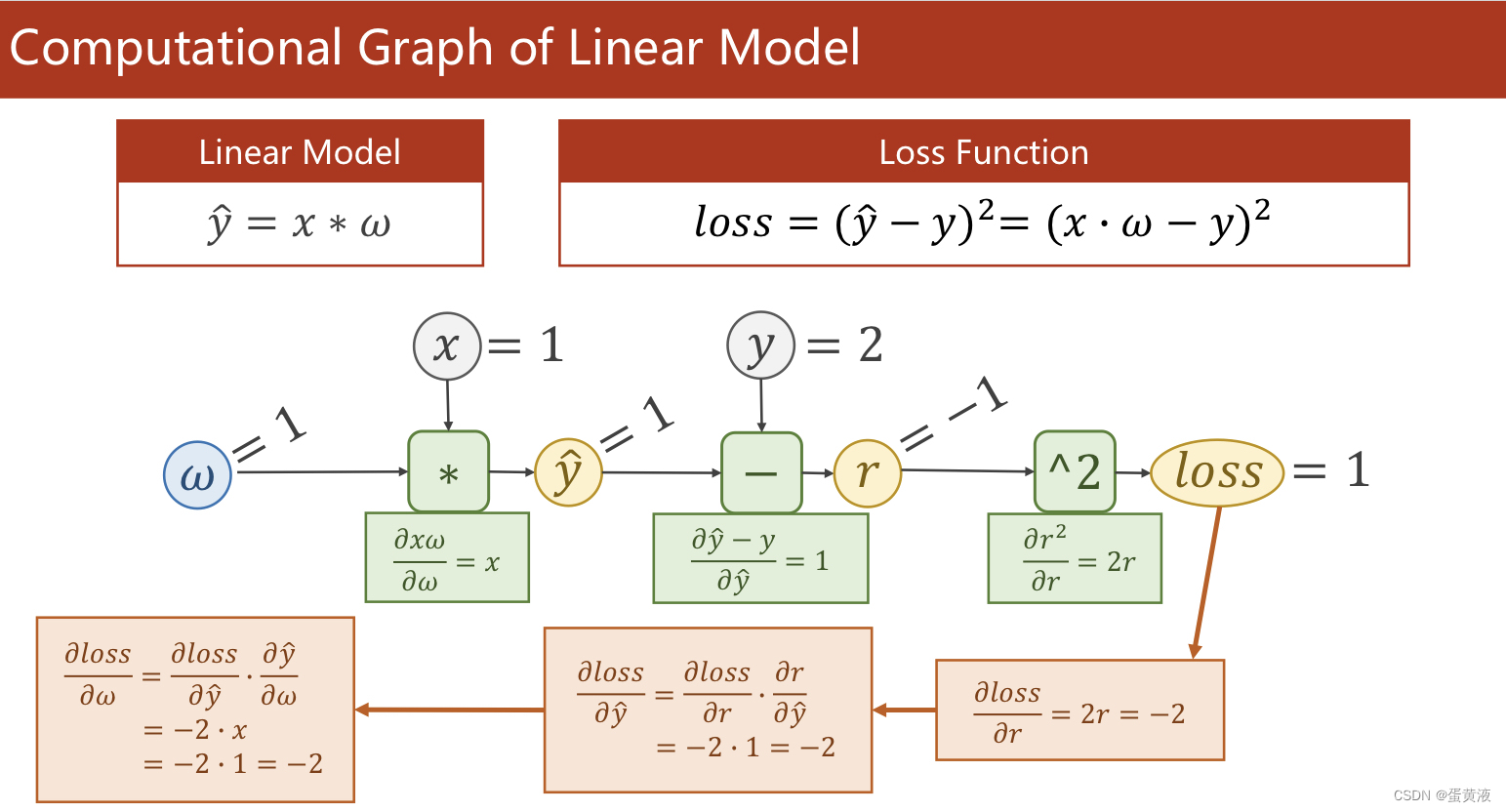
1 | import torch |
Pytorch实现线性回归
1.Prepare dataset
1 | import torch |
2.Design model using Class
重点：构造计算图
Construct loss and optimizer
Training cycle
1 | import torch |
逻辑回归
处理二分类问题
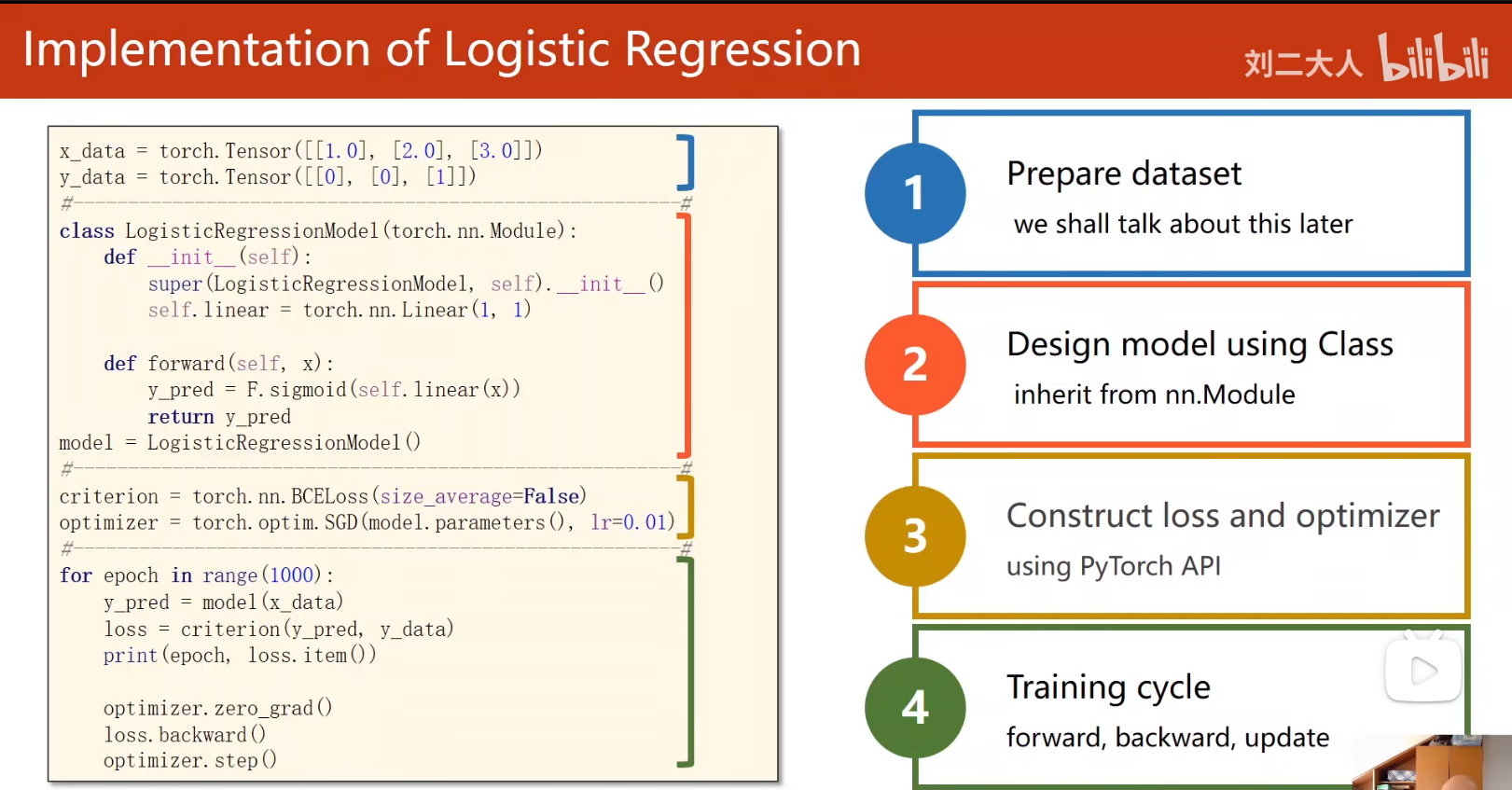
1 | #导入数据 |
每天默写一遍（
多维输入
矩阵是空间变换的函数，所以可以改变维度 神经网络是寻找一种非线性的空间变换的函数 linear可以做到空间维度的变换
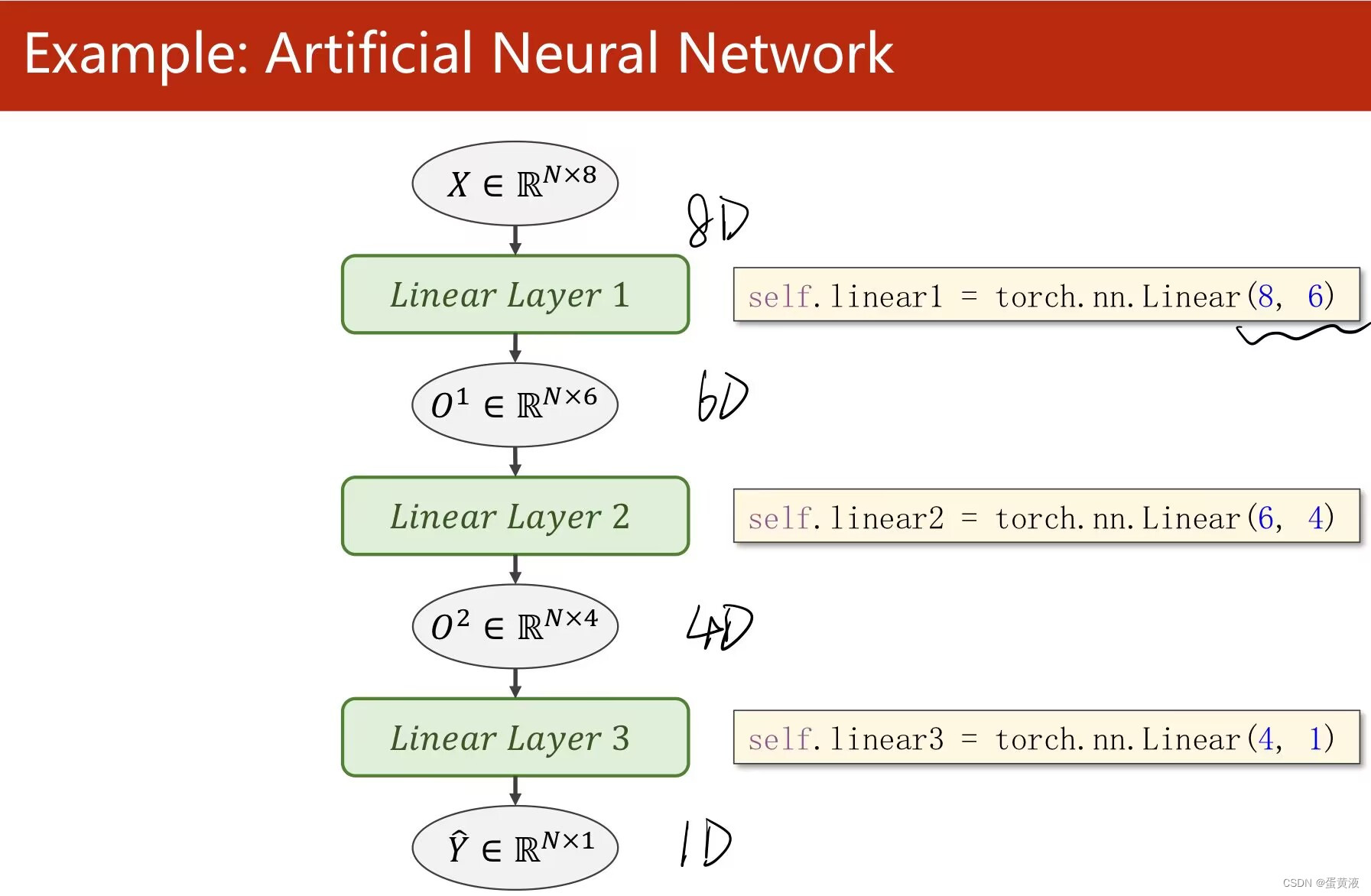
1 | import numpy as np |
创建数据集
1 | import numpy as np |
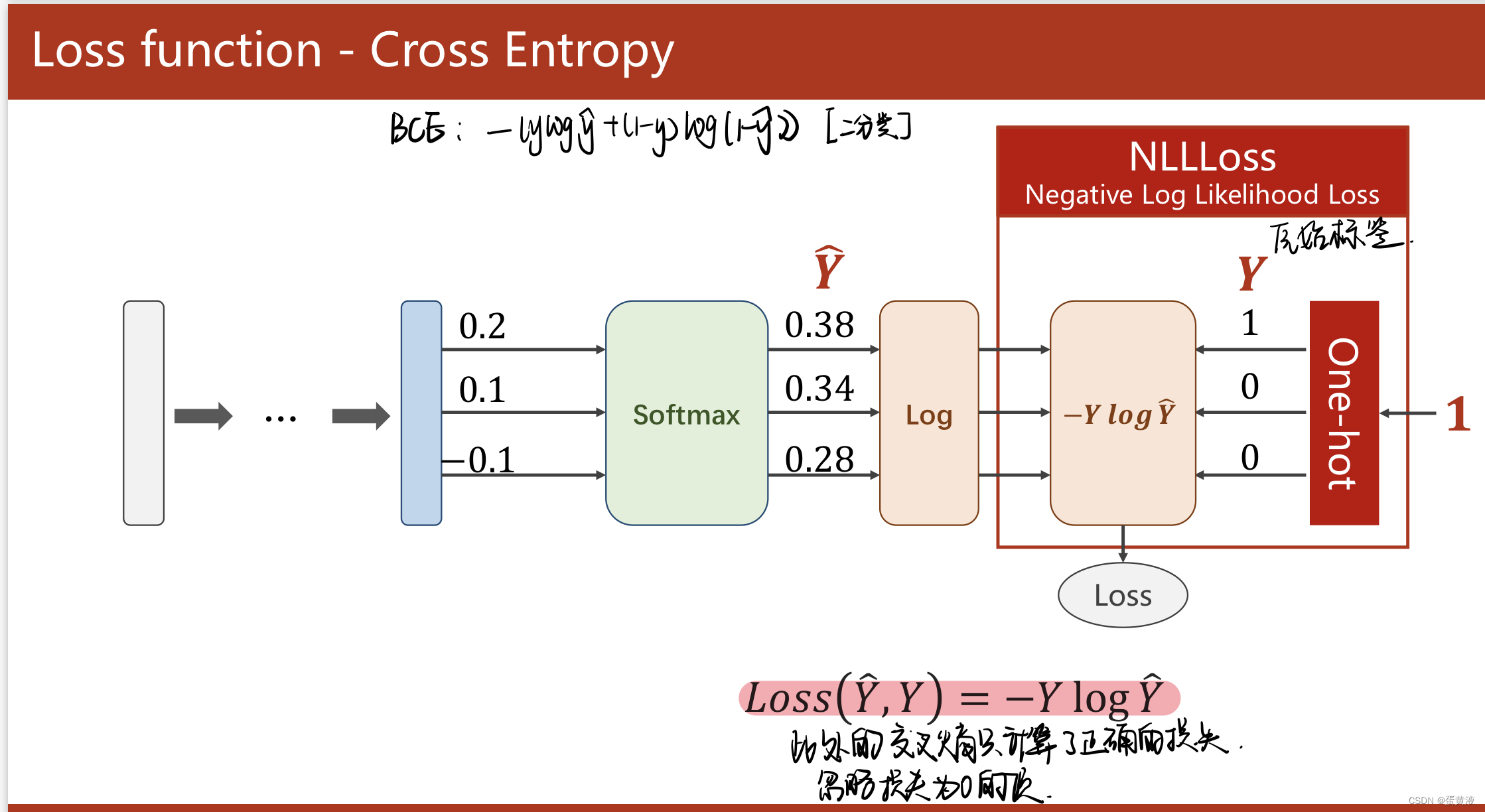
多分类
Softmax层：求指数，然后除以求和求加权 注意：交叉熵损失前计算出的结果不需要softmax激活
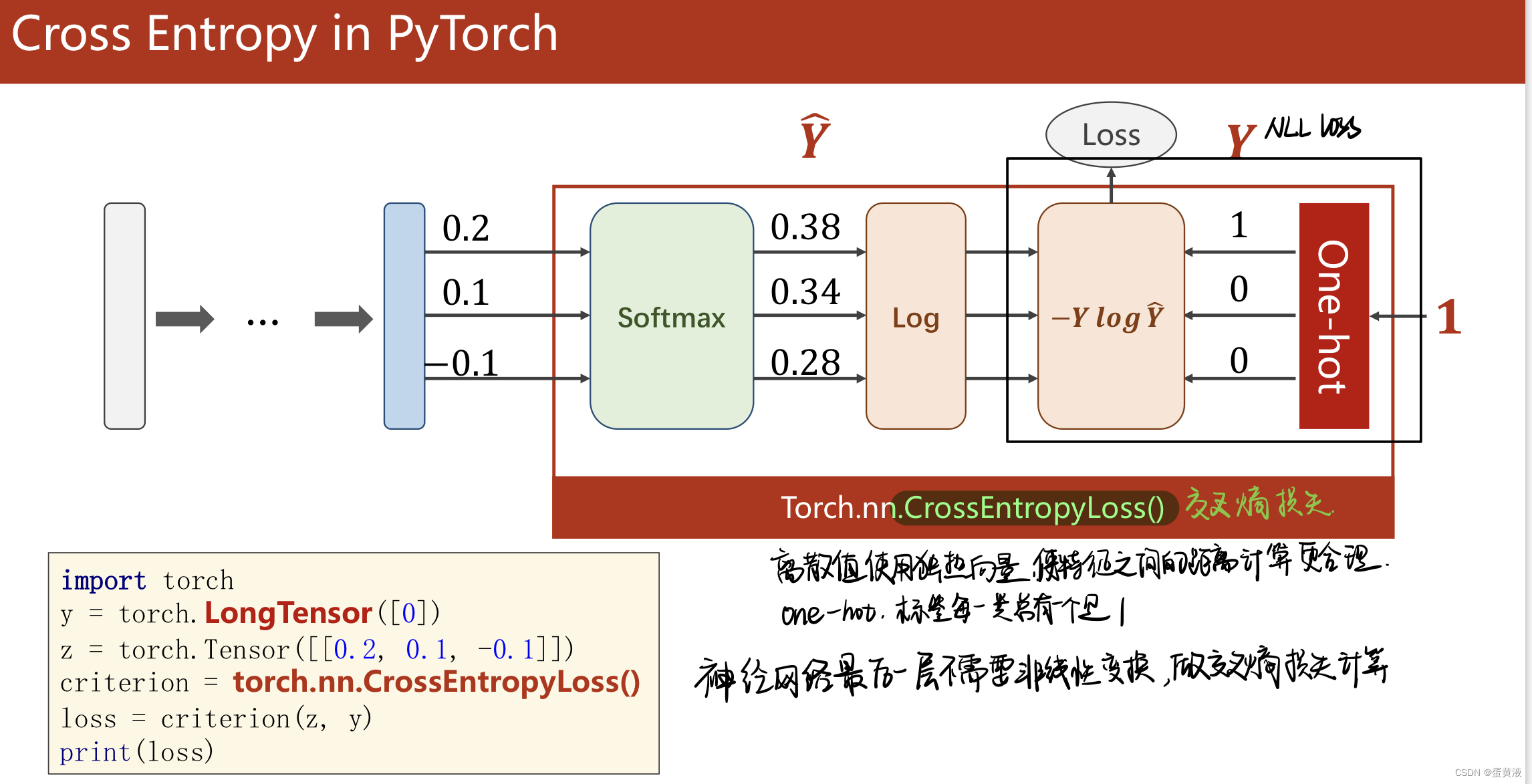
1
2
3
4
5import torch
y = torch.LongTensor([0])
z = torch.Tensor([[0.2,0.1,-0.1]])
criterion = torch.nn.CrossEntropyLoss()
loss=criterion(z,y)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91import torch
import matplotlib.pyplot as plt
from torchvision import transforms # 针对图像处理
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F # 使用ReLU
import torch.optim as optim # 优化器
#数据集准备
batch_size=64
# transform pytorch读图像时，神经网络希望输入比较小，
# pillow把图像转化为图像张量，单通道转化为多通道
transform=transforms.Compose([transforms.ToTensor(),# 转化成张量
transforms.Normalize((0.1307,),(0.3081,))])# normalize归一化，(均值，标准差)
# transform放到数据集里是为了对第i个数据集直接操作
train_dataset = datasets.MNIST(root='../dataset/mnist',
train=True,
download=True,
transform=transform)
train_loader = DataLoader(train_dataset,
shuffle=True,
batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/',
train=False,
download=True,
transform=transform)
test_loader = DataLoader(test_dataset,
shuffle=False,
batch_size=batch_size)
#构造模型
class Model(torch.nn.Module):
def __init__(self):
super(model,self).__init__()
self.l1 = torch.nn.Linear(784,512)
self.l2=torch.nn.Linear(512,256)
self.l3=torch.nn.Linear(256,128)
self.l4=torch.nn.Linear(128,64)
self.l5=torch.nn.Linear(64,10)
def forward(self,x):
x = x.view(-1, 784) # view改变张量的形式，把（N,1,28,28）变成二阶,-1表示0维度的数字不变
x=F.relu(self.l1(x))
x=F.relu(self.l2(x))
x=F.relu(self.l3(x))
x=F.relu((self.l4(x)))
return self.l5(x) #最后一层不激活
model=Model()
# 3.损失函数和优化器
criterion = torch.nn.CrossEntropyLoss() # 交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5) # 用带冲量的
# 4.训练周期+测试集
def train(epoch):
running_loss = 0.0
for batch_size, data in enumerate(train_loader, 0):
inputs, target = data # x，y
optimizer.zero_grad() # 在优化器优化之前，进行权重清零;
outputs = model(inputs)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item() # 累计loss
if batch_size % 300 == 299:
print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_size + 1, running_loss / 300))
def test():
correct = 0
total = 0
with torch.no_grad(): # 不需要计算梯度
for data in test_loader:
images, labels = data
outputs = model(images)
# 求每一行最大值的下标，返回最大值，和下标
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0) # batch_size
correct += (predicted == labels).sum().item() # 比较下标与预测值是否接近，求和表示猜对了几个
print('Accuracy on test set: %d %%' % (100 * correct / total))
if __name__ == '__main__':
for epoch in range(100):
train(epoch)
test()
卷积(basic)
padding 
stride 
pooling池化 
简单CNN 
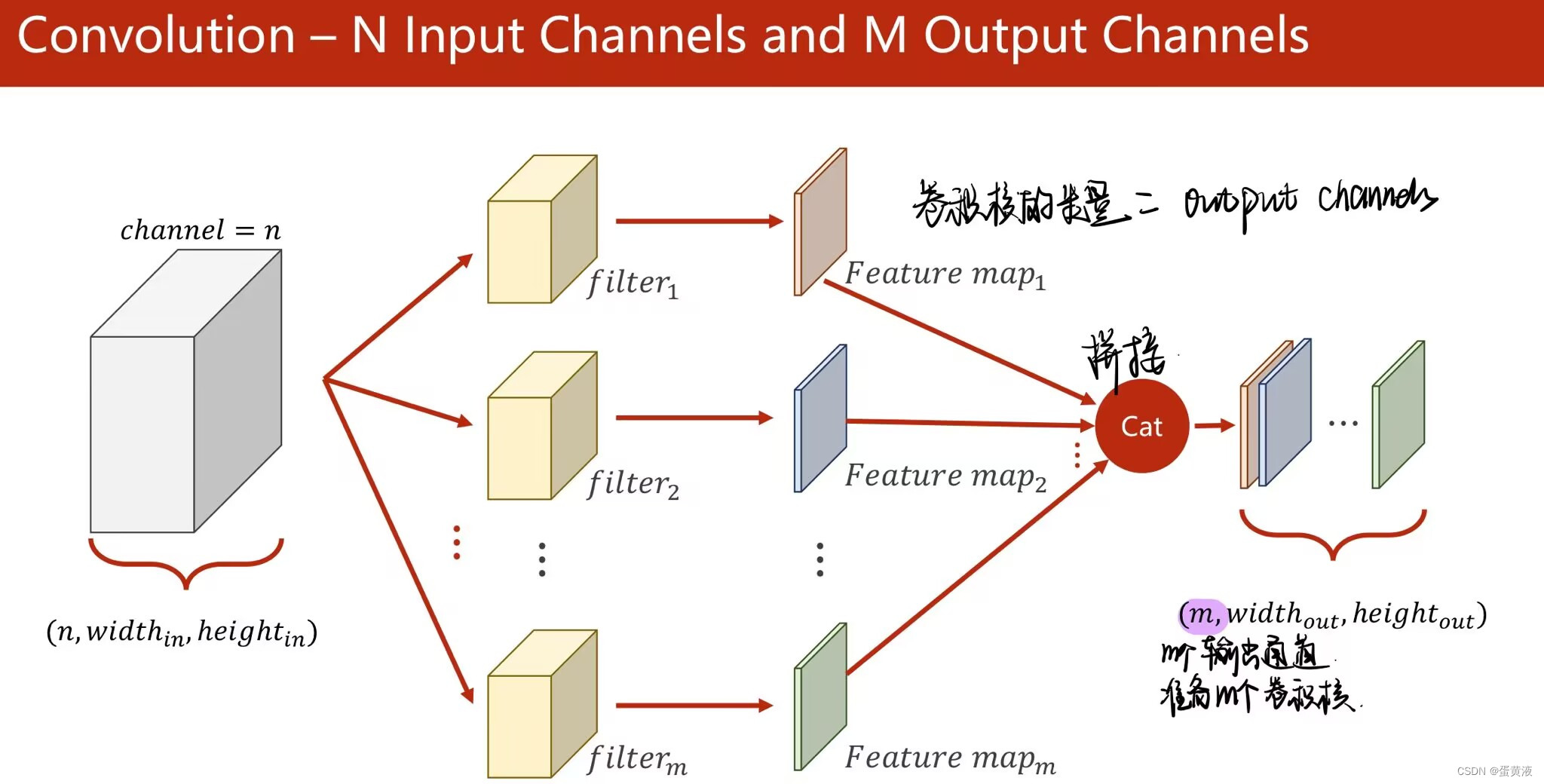
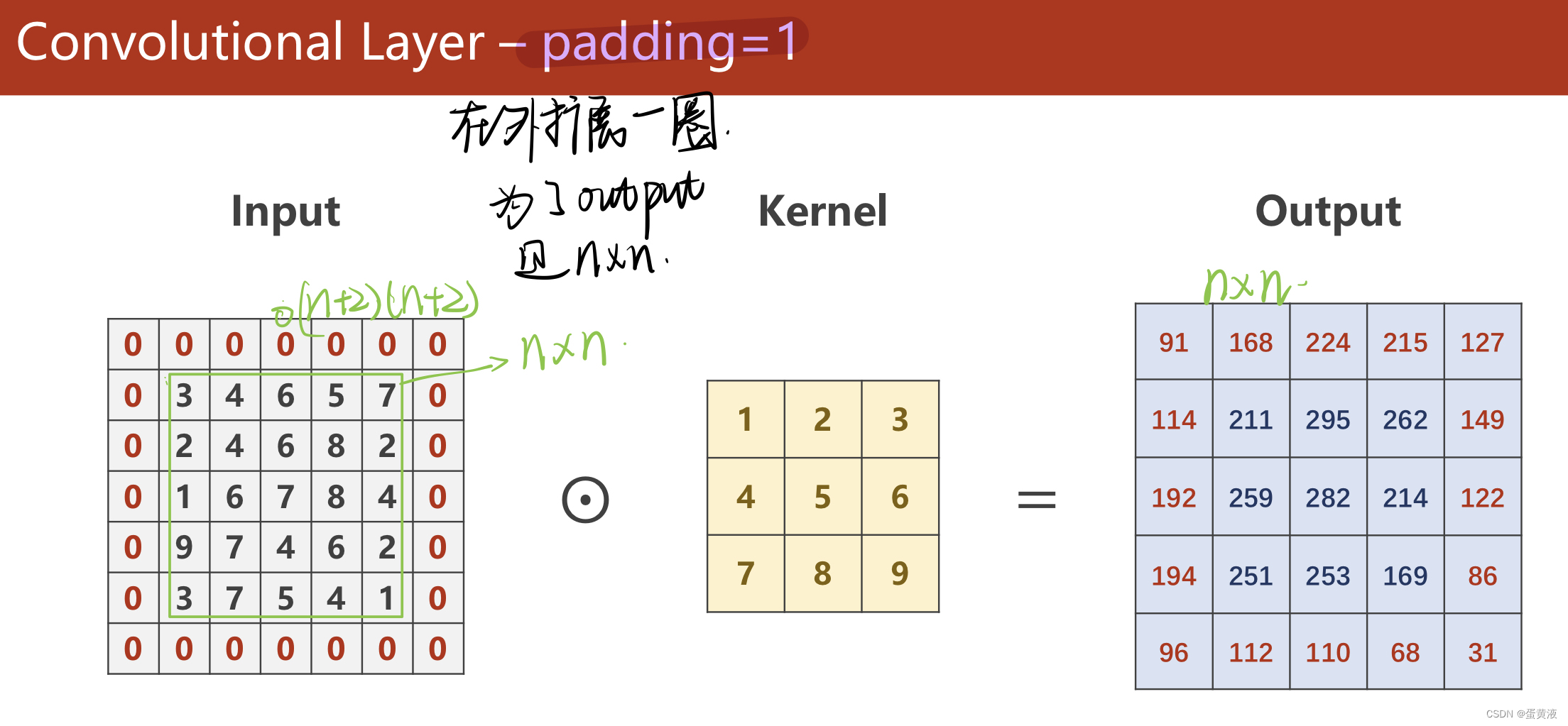
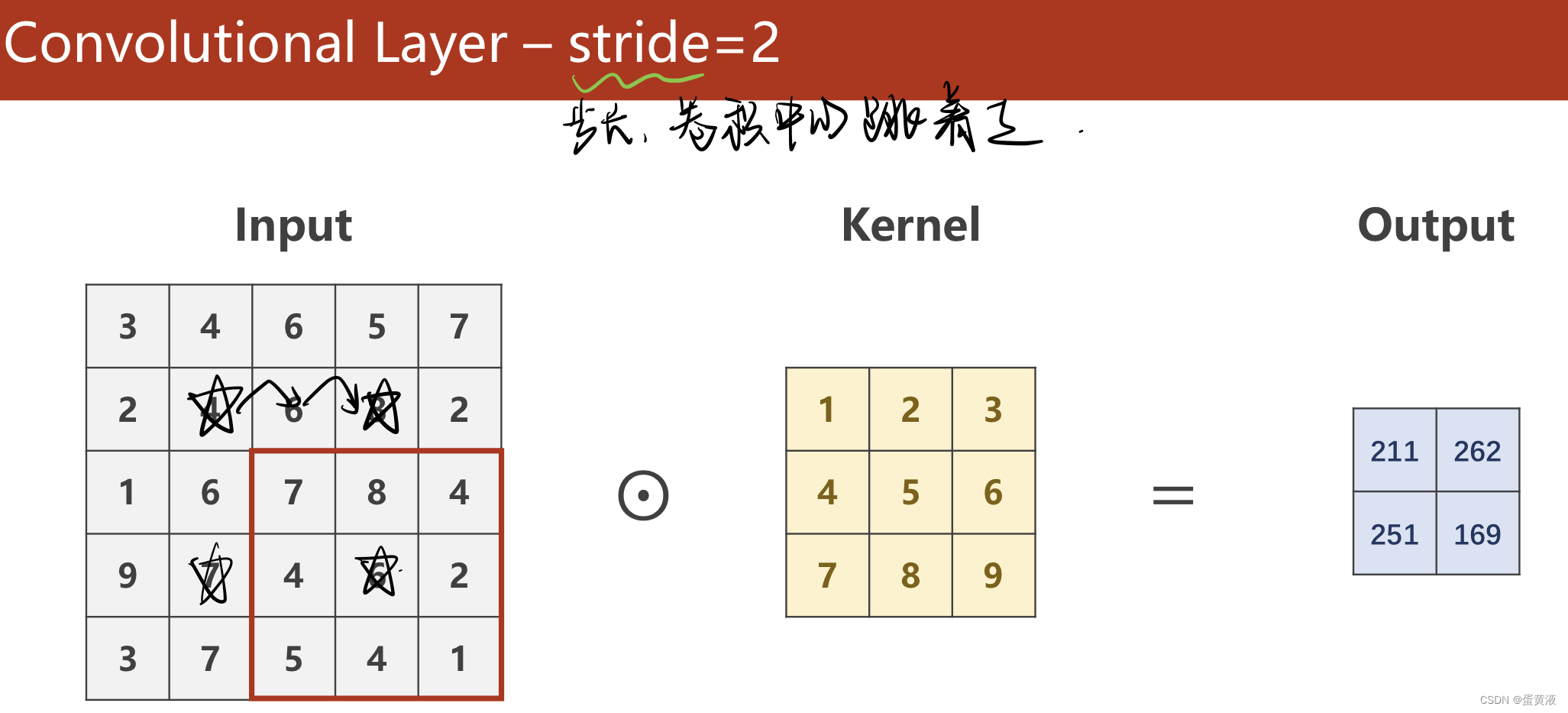
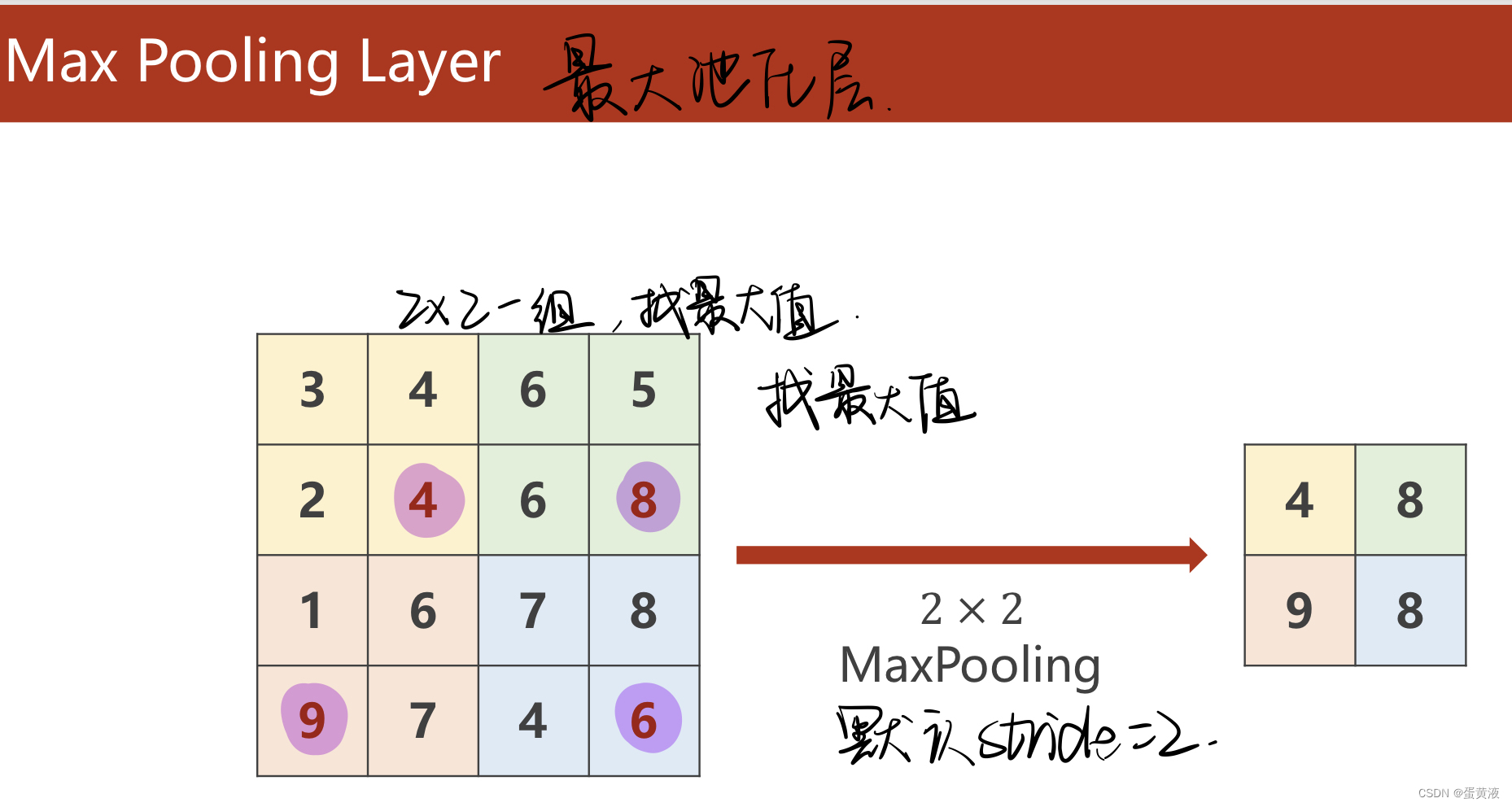
1 | import matplotlib.pyplot as plt |
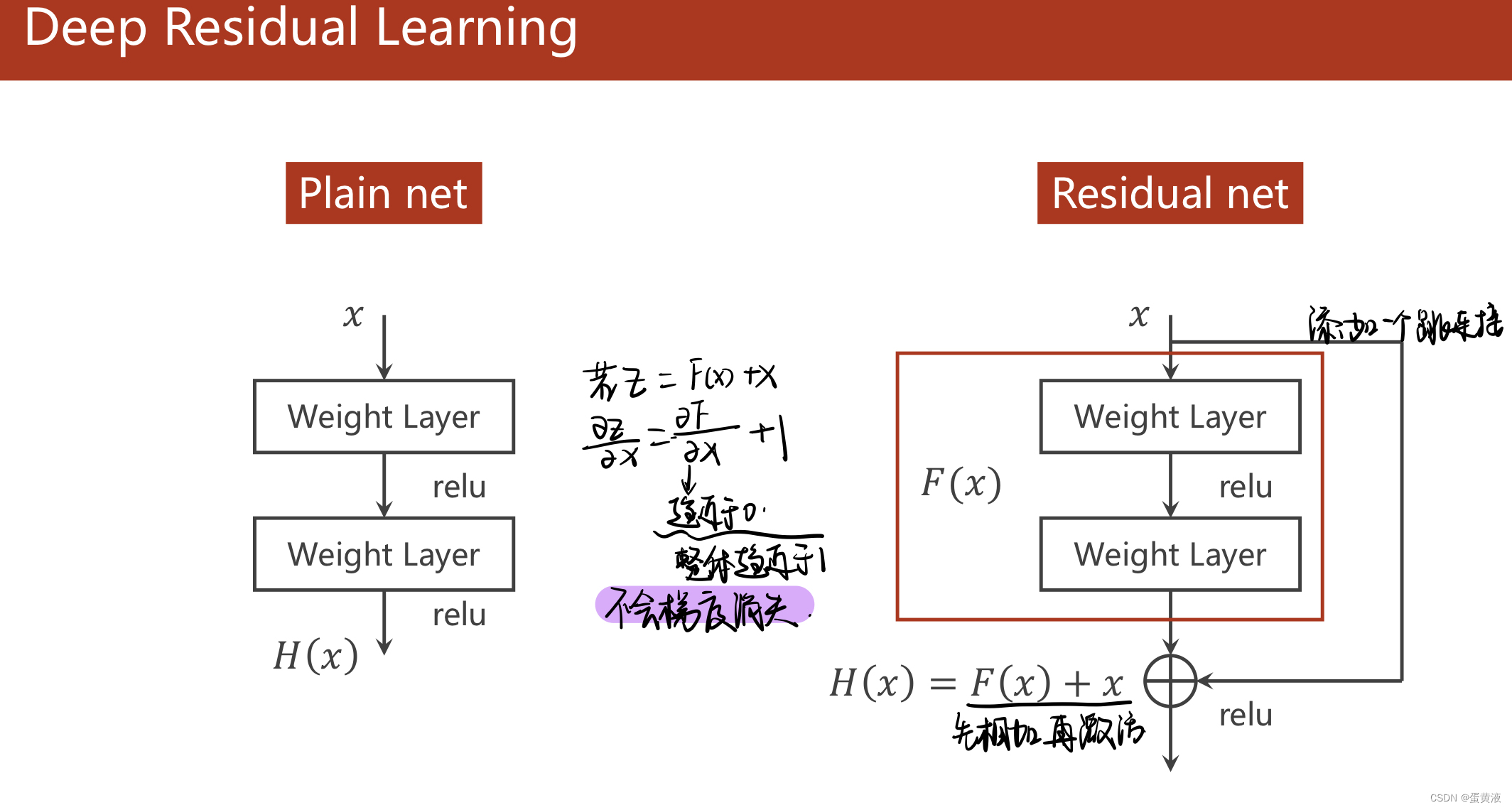
ResNet
以往的网络模型是这种Plain
Net形式：输入数据x，经过Weight
Layer(可以是卷积层，也可以是池化或者线性层)，再通过激活函数加入非线性影响因素，最后输出结果H(x)；这种方式使得H(x)对x的偏导数的值分布在（0,1）之间，这在反向传播、复合函数的偏导数逐步累乘的过程中，必然会导致损失函数L对x的偏导数的值，趋近于0，而且，网络层数越深，这种现象就会越明显，最终导致最开始的（也就是靠近输入的）层没有获得有效的权重更新，甚至模型失效；
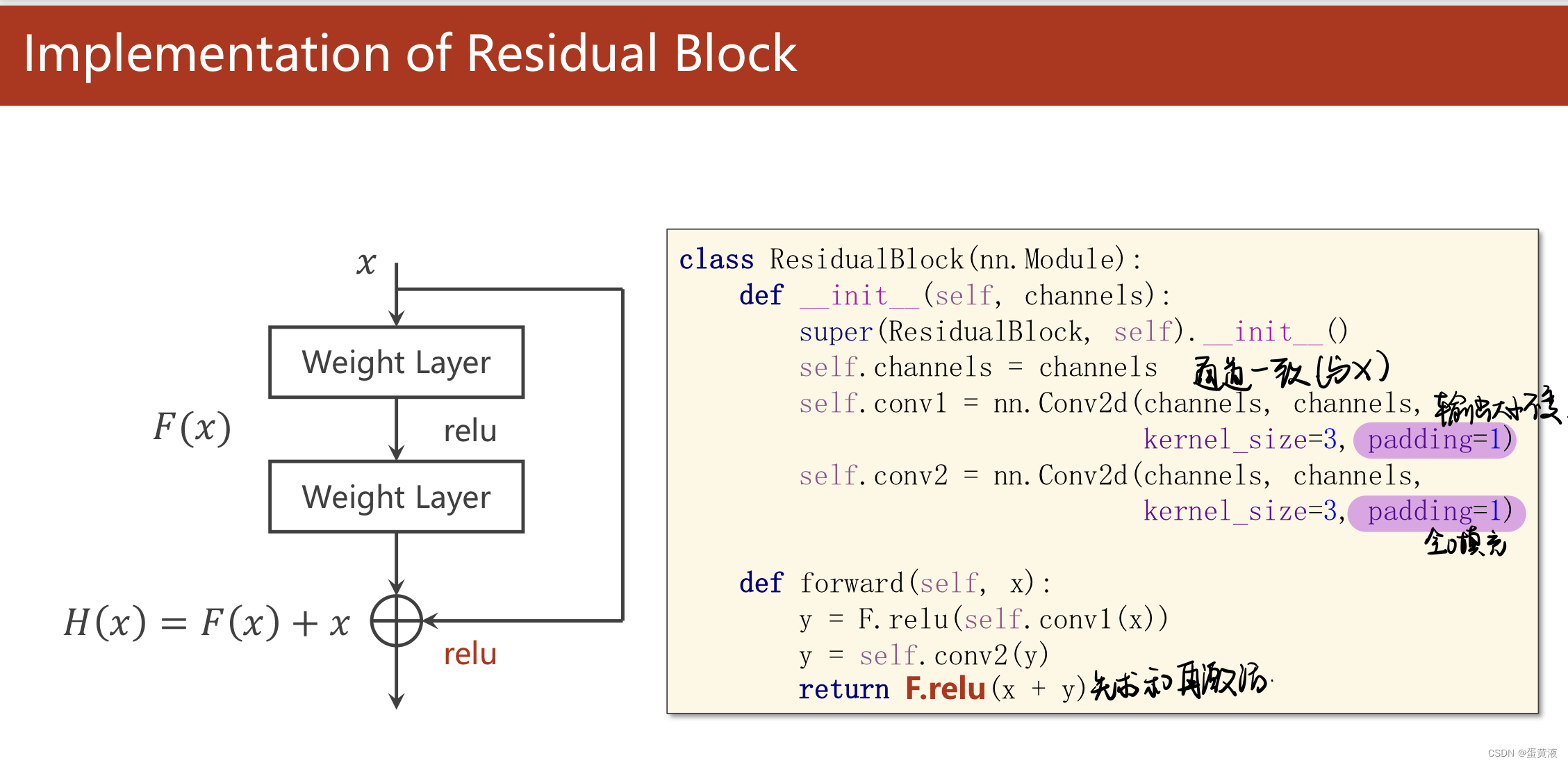
ResNet采用了一个非常巧妙的方式解决了H(x)对x的偏导数的值分布在（0,1）之间这个问题：在以往的框架中，加入一个跳跃，再原有的网络输出F(x)的基础上，将输入x累加到上面，这样一来，在最终输出H(x)对输入数据x求偏导数的时候，这个结果就会分布在（1,2）之间，这样就不怕网络在更新权重梯度累乘的过程中，出现乘积越来越趋于0而导致的梯度消失问题；
注意：resblock前后的输入和输出的纬度要一样
RNN(basic)
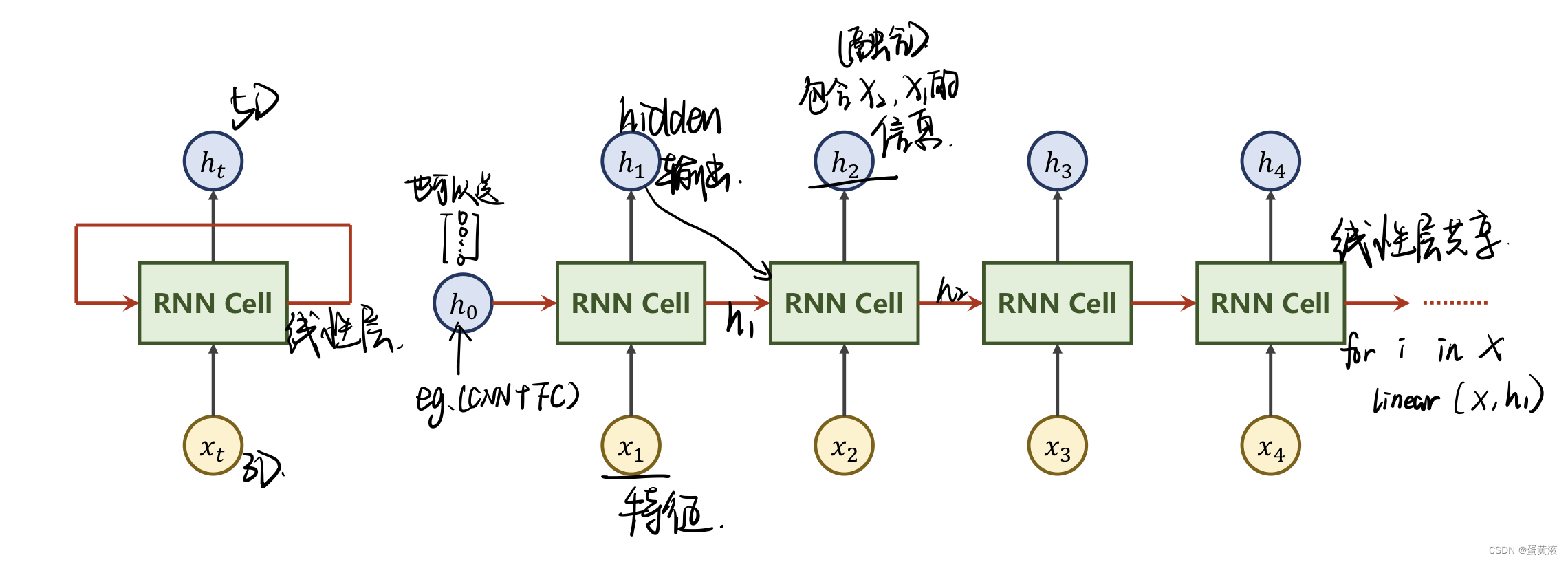
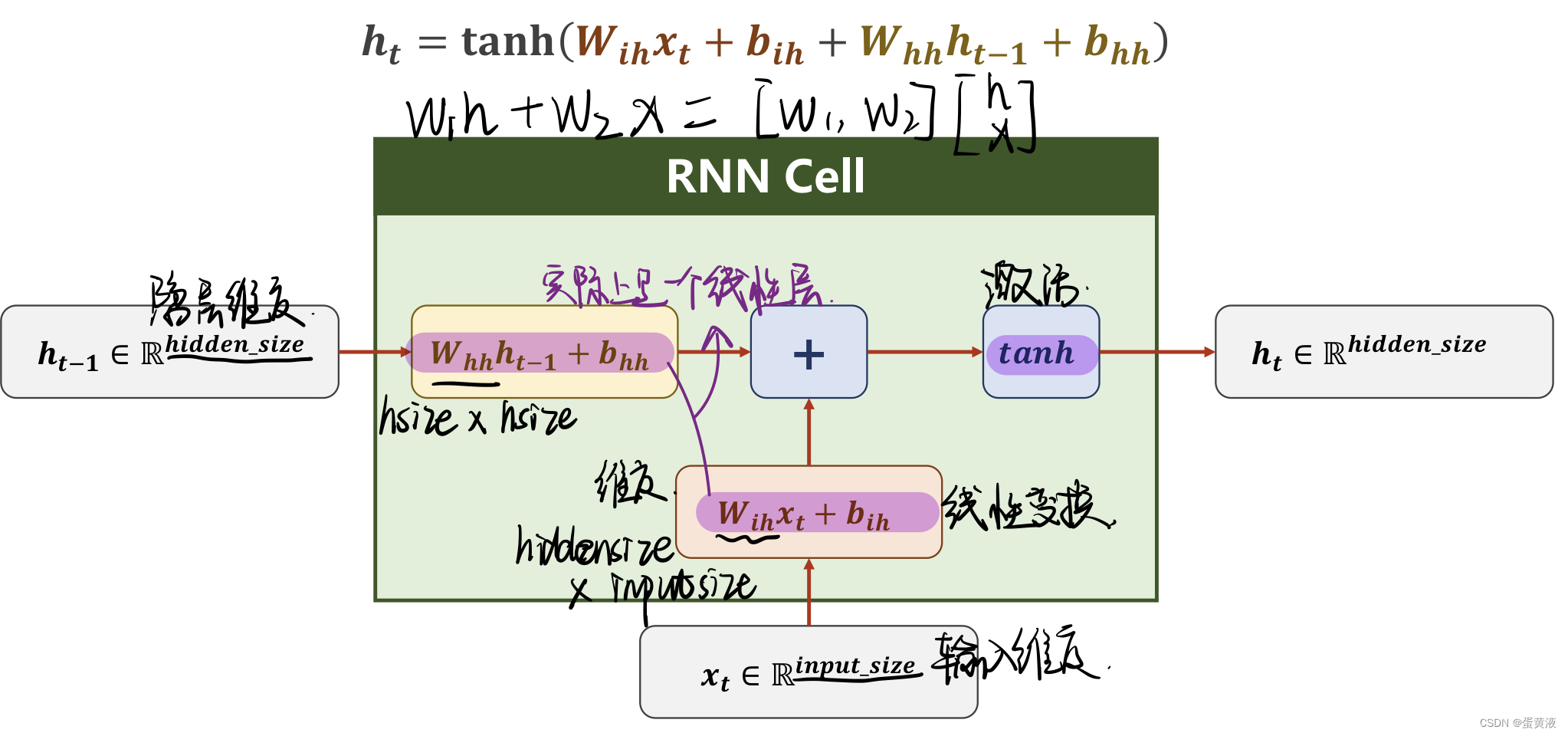
1 | import torch |
hallo->ohlol 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82# 使用RNN
import torch
from torch import nn, optim
from torchvision import datasets
from torch.utils.data import DataLoader
from torchvision import transforms
import torch.nn.functional as F
import matplotlib.pyplot as plt
input_size = 4
hidden_size = 4
num_layers = 1
batch_size = 1
seq_len = 5
# 准备数据
idx2char = ['e', 'h', 'l', 'o']
x_data = [1, 0, 2, 2, 3] # hello
y_data = [3, 1, 2, 3, 2] # ohlol
one_hot_lookup = [[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]] # 分别对应0,1,2,3项
x_one_hot = [one_hot_lookup[x] for x in x_data] # 组成序列张量
print('x_one_hot:', x_one_hot)
# 构造输入序列和标签
inputs = torch.Tensor(x_one_hot).view(seq_len, batch_size, input_size)
labels = torch.LongTensor(y_data) # labels维度是: (seqLen * batch_size ，1)
# design model
class Model(torch.nn.Module):
def __init__(self, input_size, hidden_size, batch_size, num_layers=1):
super(Model, self).__init__()
self.num_layers = num_layers
self.batch_size = batch_size
self.input_size = input_size
self.hidden_size = hidden_size
self.rnn = torch.nn.RNN(input_size=self.input_size,
hidden_size=self.hidden_size,
num_layers=self.num_layers)
def forward(self, input):
hidden = torch.zeros(self.num_layers, self.batch_size, self.hidden_size)
out, _ = self.rnn(input, hidden)
# 为了能和labels做交叉熵，需要reshape一下:(seqlen*batchsize, hidden_size),即二维向量，变成一个矩阵
return out.view(-1, self.hidden_size)
net = Model(input_size, hidden_size, batch_size, num_layers)
# loss and optimizer
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.05)
# train cycle
if __name__ == '__main__':
epoch_list = []
loss_list = []
for epoch in range(20):
optimizer.zero_grad()
# inputs维度是: (seqLen, batch_size, input_size) labels维度是: (seqLen * batch_size * 1)
# outputs维度是: (seqLen, batch_size, hidden_size)
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
_, idx = outputs.max(dim=1)
idx = idx.data.numpy()
print('Predicted: ', ''.join([idx2char[x] for x in idx]), end='')
print(',Epoch [%d/20] loss=%.3f' % (epoch + 1, loss.item()))
epoch_list.append(epoch)
loss_list.append(loss.item())
plt.plot(epoch_list, loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
